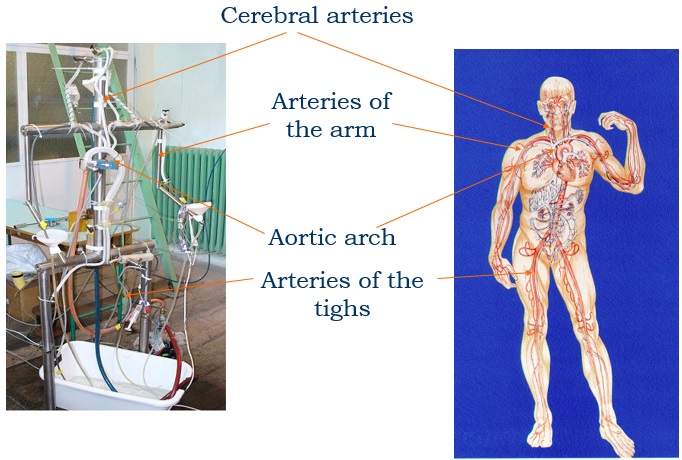
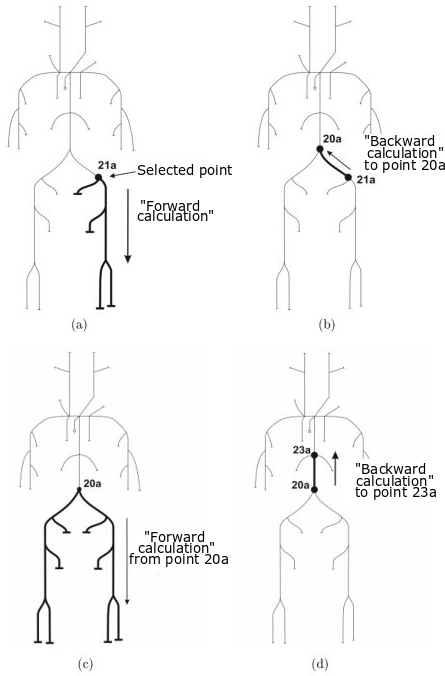
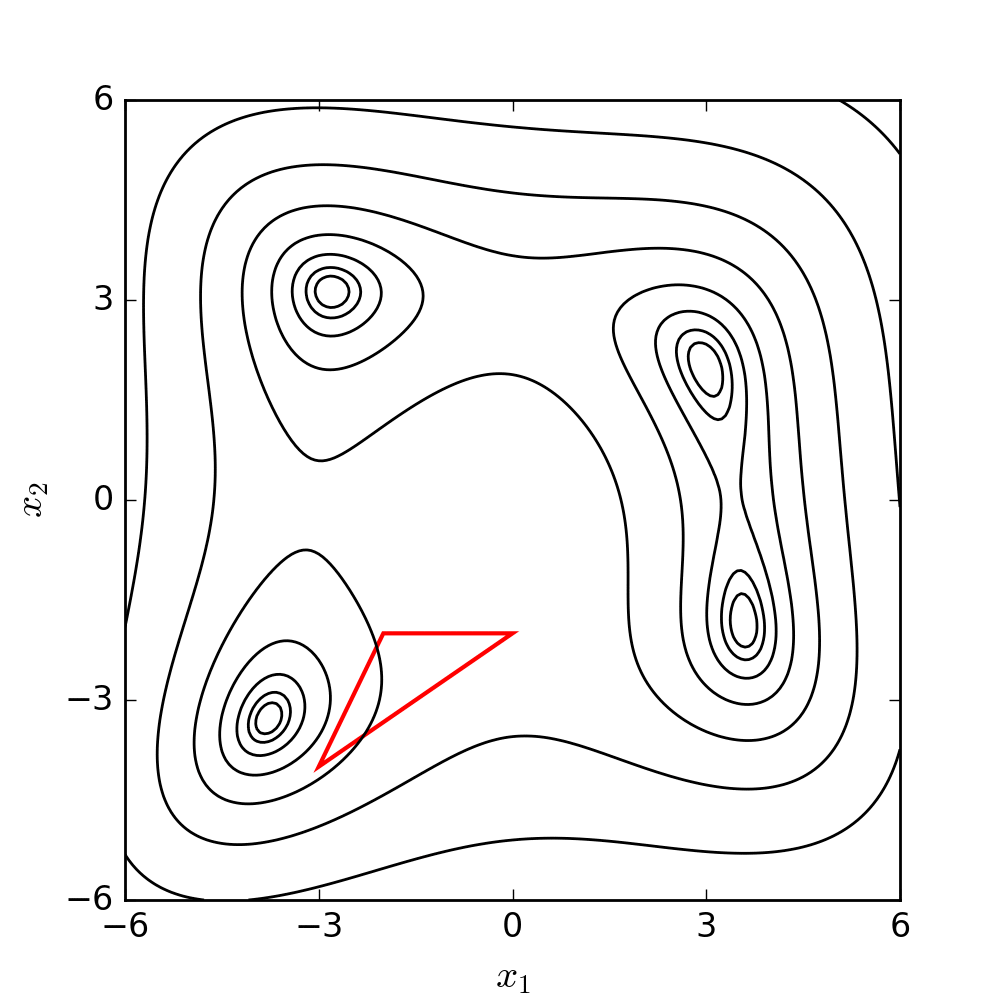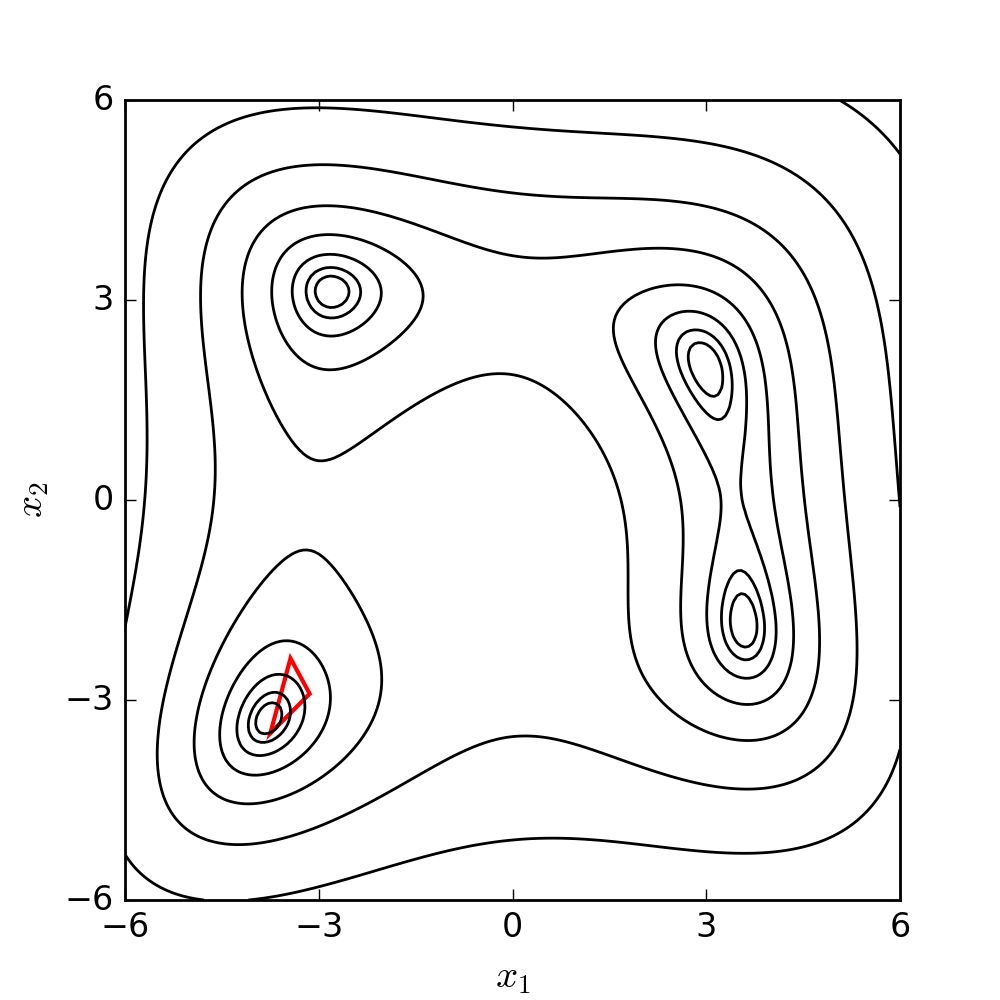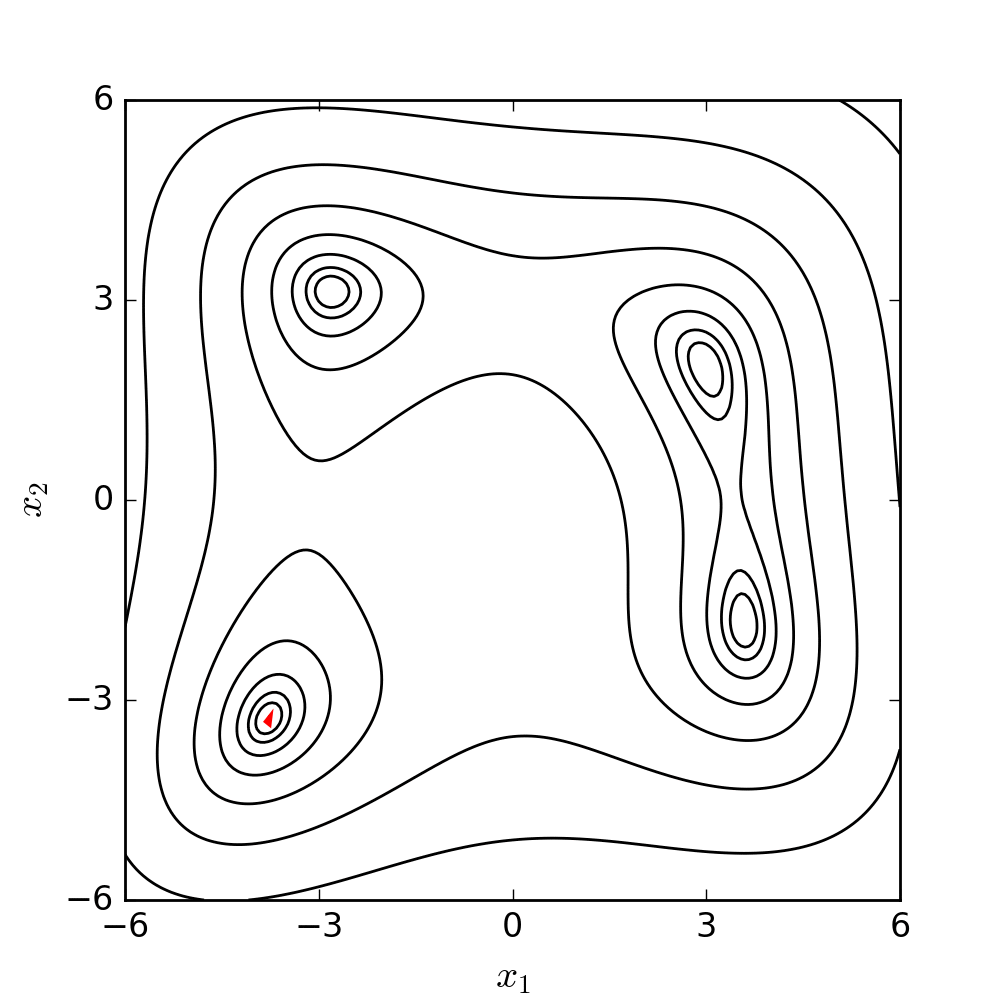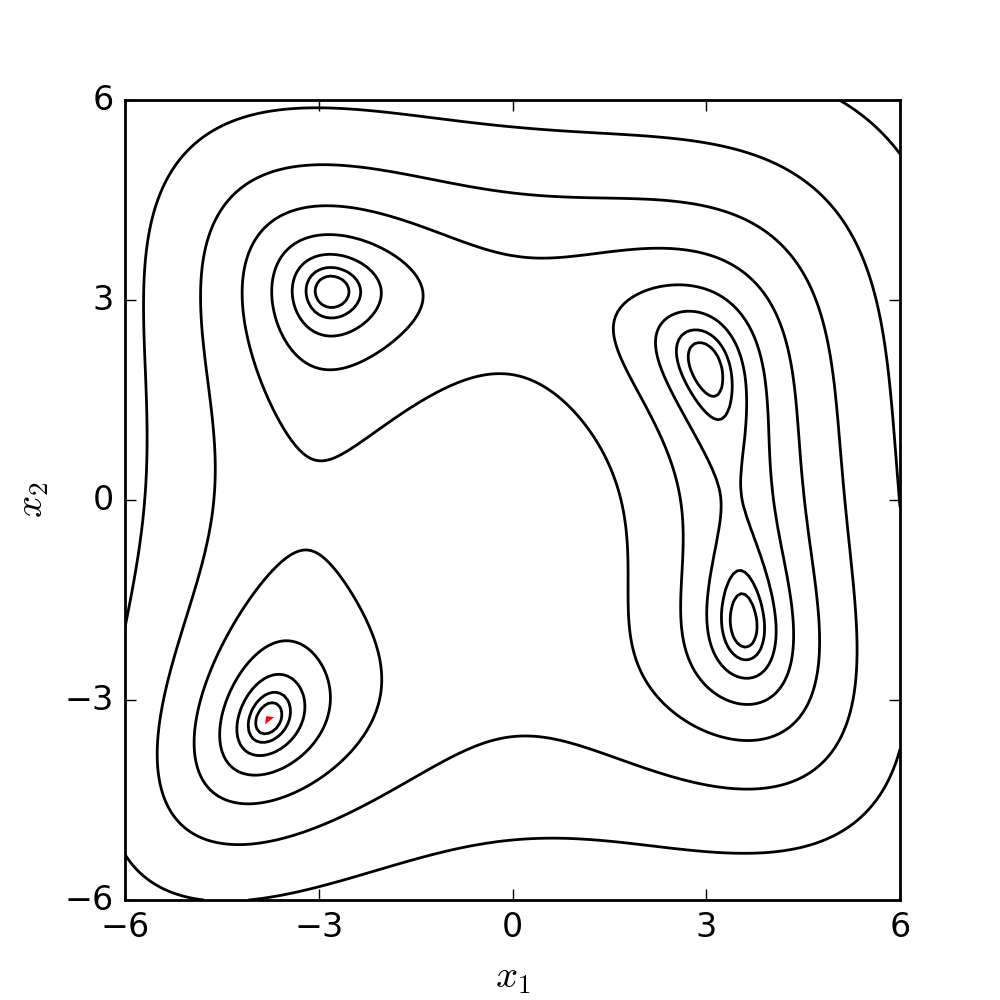
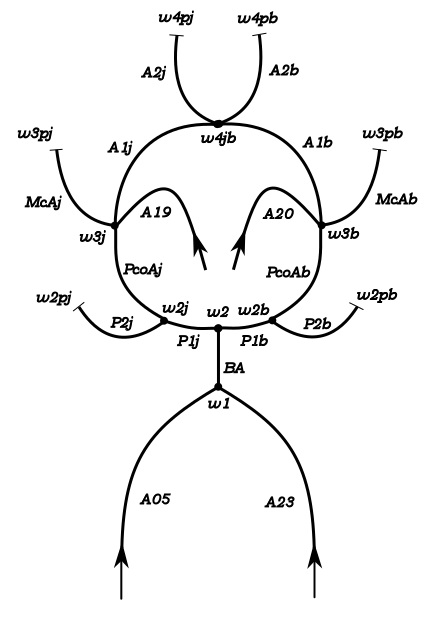
Experimental model of the arterial system
In the early stages of the research we constructed a simplified laboratory model of the arterial system with easily deformable plastic tubes and a membrane pump generating periodic flow. The measurements made on this model verified the correctness of our calculation procedure.
 Hemodynamics Research Group
Hemodynamics Research Group