-
Papers in high impact journals
-
Klapcsik, K., Hegedűs, F. (2019): Study of non-spherical bubble oscillations under acoustic irradiation in viscous liquid. Ultrason. Sonochem., (In Press)
-
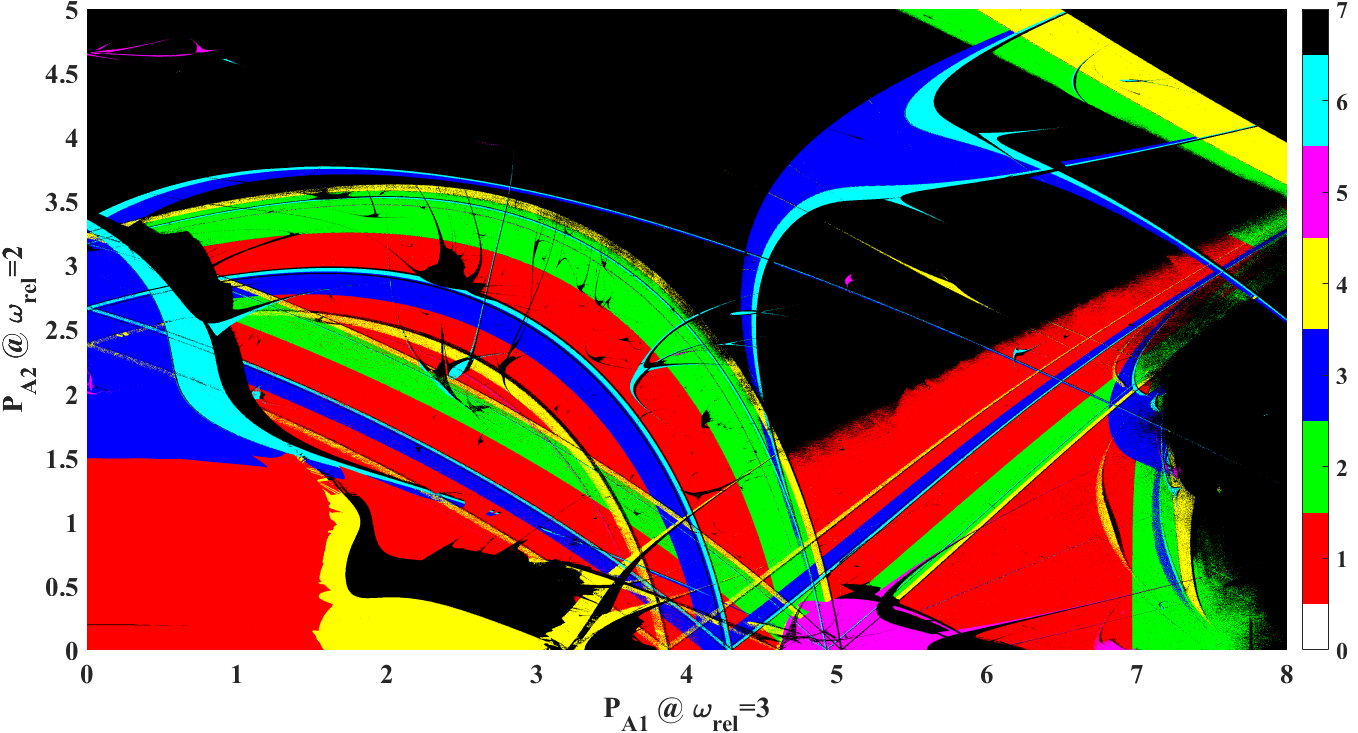
Klapcsik, K., Varga, R., Hegedűs, F. (2018): Bi-parametric topology of subharmonics of an asymmetric bubble oscillator at high dissipation rate. Nonlinear Dyn., 94(4), pp. 2373-2389.
-
Hegedűs, F., Lauterborn, W., Parlitz, U., Mettin, R. (2018): Non-feedback technique to directly control multistability in nonlinear oscillators by dual-frequency driving. Nonlinear Dyn., 94(1), pp. 273-293.
-
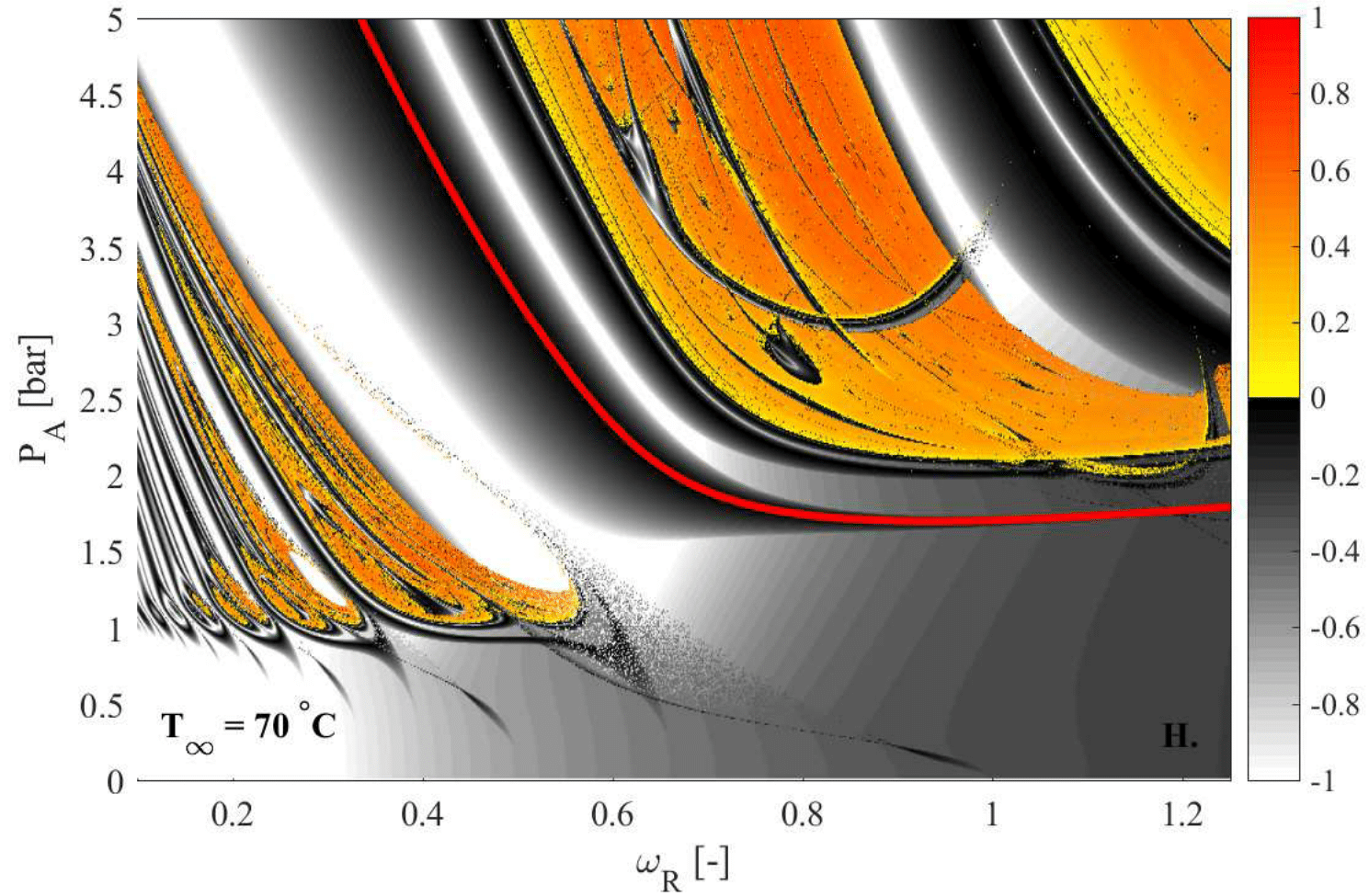
Hegedűs, F., Kalmár, Cs. (2018): Dynamic stabilization of an asymmetric nonlinear bubble oscillator. Nonlinear Dyn., 94(1), pp. 307-324.
-
Klapcsik, K., Hegedűs, F. (2017): The effect of high viscosity on the evolution of the bifurcation set of a periodically excited gas bubble. Chaos Solitons Fract., 104, pp. 198-208.
-
Varga, R., Hegedűs, F. (2016): Classification of the bifurcation structure of a periodically driven gas bubble. Nonlinear Dyn., 86(2), pp. 1239-1248.
-
Garen, W., Hegedűs, F., Kai, Y., Koch, S., Meyerer, B., Neu, W., Teubner, U. (2016): Shock wave emission during the collapse of cavitation bubbles. Shock Waves, 26(4), pp. 385-394.
-
Hegedűs, F. (2016): Topological analysis of the periodic structures in a harmonically driven bubble oscillator near Blake's critical threshold: Infinite sequence of two-sided Farey ordering trees. Phys. Lett. A, 380(9-10), pp. 1012-1022.
-
Hegedűs, F., Klapcsik, K. (2015): The effect of high viscosity on the collapse-like oscillation of a harmonically excited gas bubble. Ultrason. Sonochem., 27, pp. 153-164.
-
Hegedűs, F. (2014): Stable bubble oscillations beyond Blake’s critical threshold. Ultrasonics, 54(4), pp. 1113-1121.
-
Hegedűs, F., Koch, S., Garen, W., Pandula, Z., Paál, G., Kullmann, L., Teubner, U. (2013): The effect of high viscosity on compressible and incompressible Rayleigh—Plesset bubble models. Int. J. Heat Fluid Flow, 42, pp. 200-208.
-
Hegedűs, F., Hős, C., Kullmann, L. (2013): Stable period 1,2 and 3 structures of the harmonically excited Rayleigh—Plesset equation applying low ambient pressure. IMA J. Appl. Math., 78(6), pp. 1179-1195.
-
Koch, S., Garen, W., Hegedűs, F., Neu, W., Reuter, R., Teubner, U. (2012): Time-resolved measurements of shock-induced cavitation bubbles in liquids. Appl. Phys. B-Lasers O., 108(2), pp. 345-351.
-
Hegedűs, F., Hős, C., Kullmann, L. (2010): Influence of heat transfer on the dynamic response of a spherical gas/vapour bubble. Int. J. Heat Fluid Flow, 31(6), pp. 1040-1049.