Edge tone
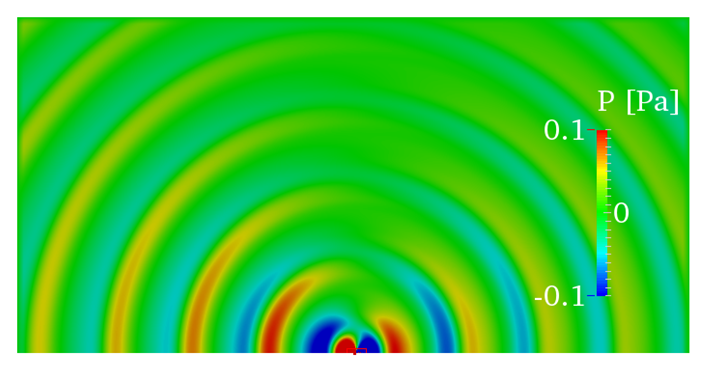
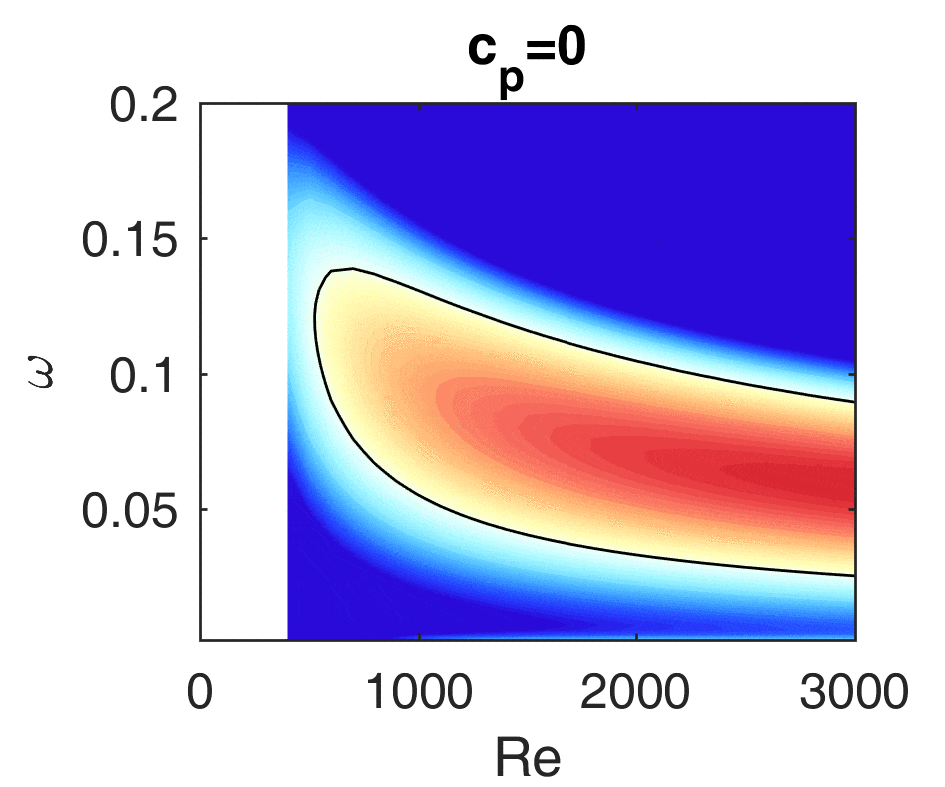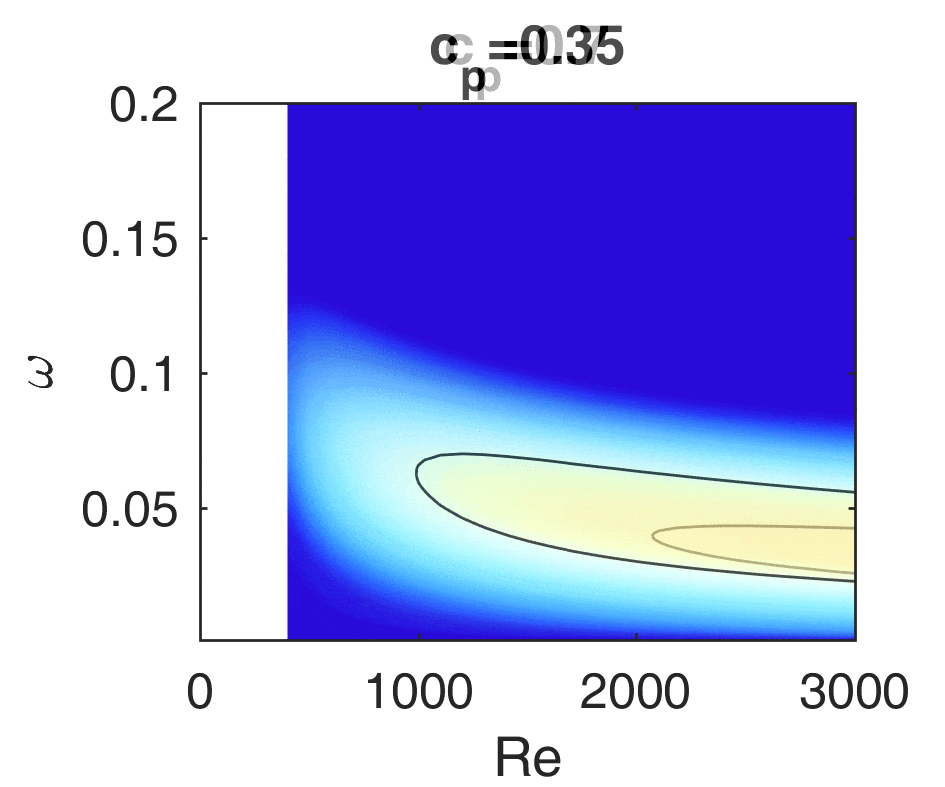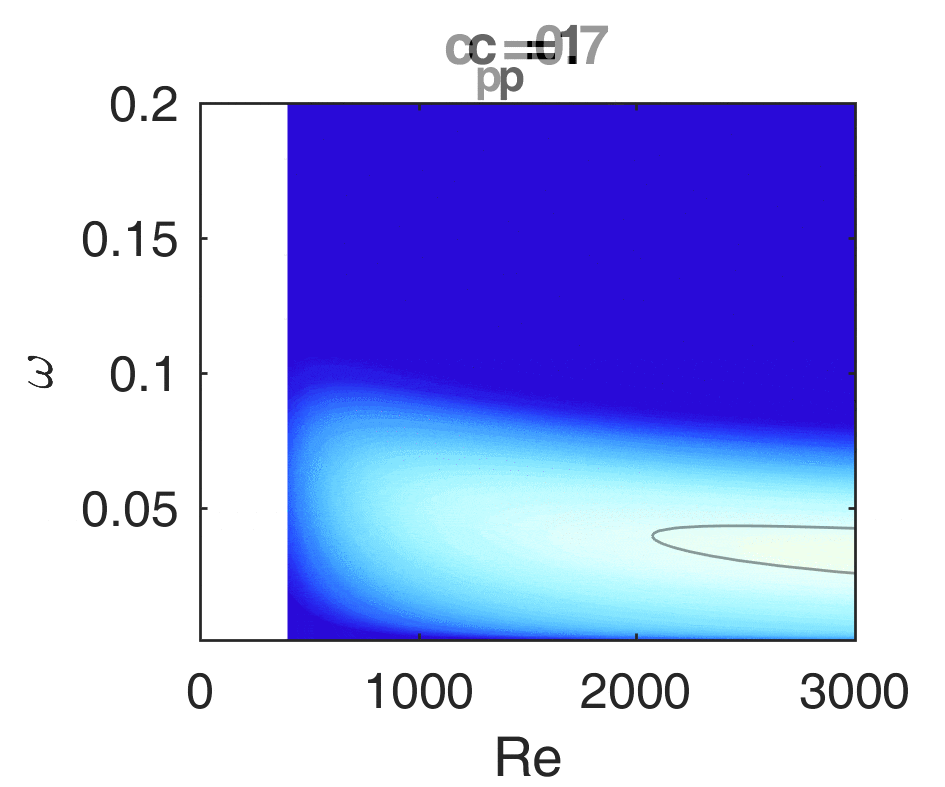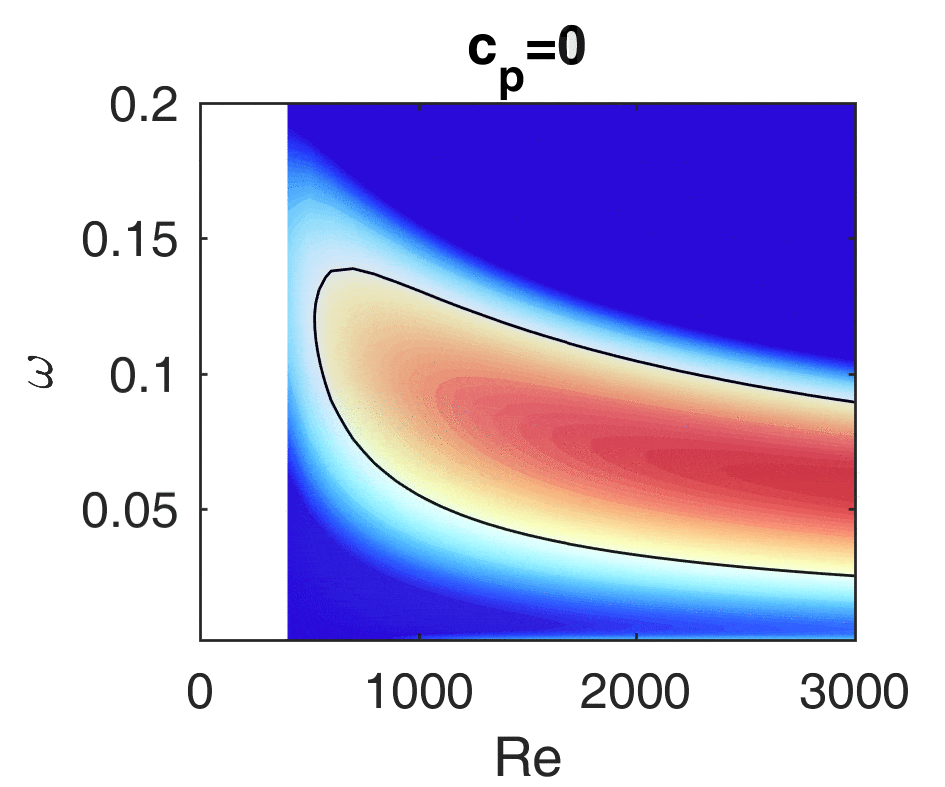
If a plane jet impinges on a wedge, it starts to swing with a well-defined frequency and it may also emit sound. This configuration is called edge tone, and it occurs among others in wind instruments (organ pipe, recorder) but it can also be used to homogenise heterogeneous mixtures. In other cases the goal is to extinguish the oscillations since they may be harmful for example at the tongue of centrifugal pumps or in Y-branches. The plane jet is in itself unstable, the amplitude of small disturbances increases exponentially streamwise from the jet exit. This means that an arbitrarily small disturbance that is always present in practice will be significantly amplified and will be detectable. If we place a wedge in the jet, then this disturbance may be fed back to the initial part of the jet, close to the jet exit, leading to an oscillation of a well-defined frequency. The exact mechanism of the feedback is not yet known. Our research group could model the oscillations of the jet using the stability analysis methods of fluid mechanics. We verified the increased sensitivity of the jet close to the exit and we discovered a new oscillation mode near the exit. The figure shows the oscillation of the jet calculated by the Orr-Sommerfeld equation. Furthermore, we worked out methods to model the acoustic and the vortex excitement which may play a role in the feedback. They have been compared with experiments.
 Flow stability research group
Flow stability research group