Parallel prefix sum

• Röviden: scan algoritmus
• Alapvető építőelem a párhuzamos algoritmusok között
• Definíció:
• tömb: $[a_0, a_1, ..., a_{n-1}]$
• asszociatív művelet: ◯
• identitás érték: I
• A scan művelet a tömbön:
• $[◯, a_0, (a_0 ◯ a_1), ..., (a_0, a_1, .., a_{n-2})]$

Parallel prefix sum

• Tehát ha az ◯ operátor például az összeadás:
• A [3 1 7 0 4 1 6 3] tömbből
• [0 3 4 11 11 15 16 22] tömb lesz.
• Megkülönböztetünk inclusive és exclusive scan-t.
• Felhasználási példák: rendezés(pl. leszámláló), sztring összehasonlítás, lexikális analízis, stream compaction ...stb.

Parallel reduction

• Ez egy egyszerűsített feladat.
• A tömbből most csak 1 adatot szeretnénk kinyerni:
• pl.: max reduction: a legnagyobb értékű elem a tömbben.
• pl.: sum reduction: a tömb elemeinek az összege.
• A redukció eredményét tipikusan a tömb 0. elemeként tároljuk.
• Megj.: A többi elemre semmit nem követelünk meg.

Parallel reduction

• Hasonlóan működik, mint a foci VB selejtező.
• A csapatok kettessével mérkőznek (bináris ◯ operátor).
• Ha 32 csapat van, az első körben 16 eredmény születik, a másodikban 8 ...stb.($log_2$ mélységű fa).
• Hatékony -> 1024 csapatból is 10 fordulóból megvan a győztes (persze kell 512 focipálya).
• Legyen az operátorunk most az összeadás (◯ = +).

Parallel reduction - kernel

• Az input tömb a globális memóriában van.
• Minden block egy részt a shared memóriába másol, és ott redukálja.
• Rekurzívan felezgetjük az aktív szálak számát az elemszám feleződésével.
• (A kódrészet értelemszerűen nem tartlamazza a shared memóriába másolást.)

Parallel reduktion - szemléltetés

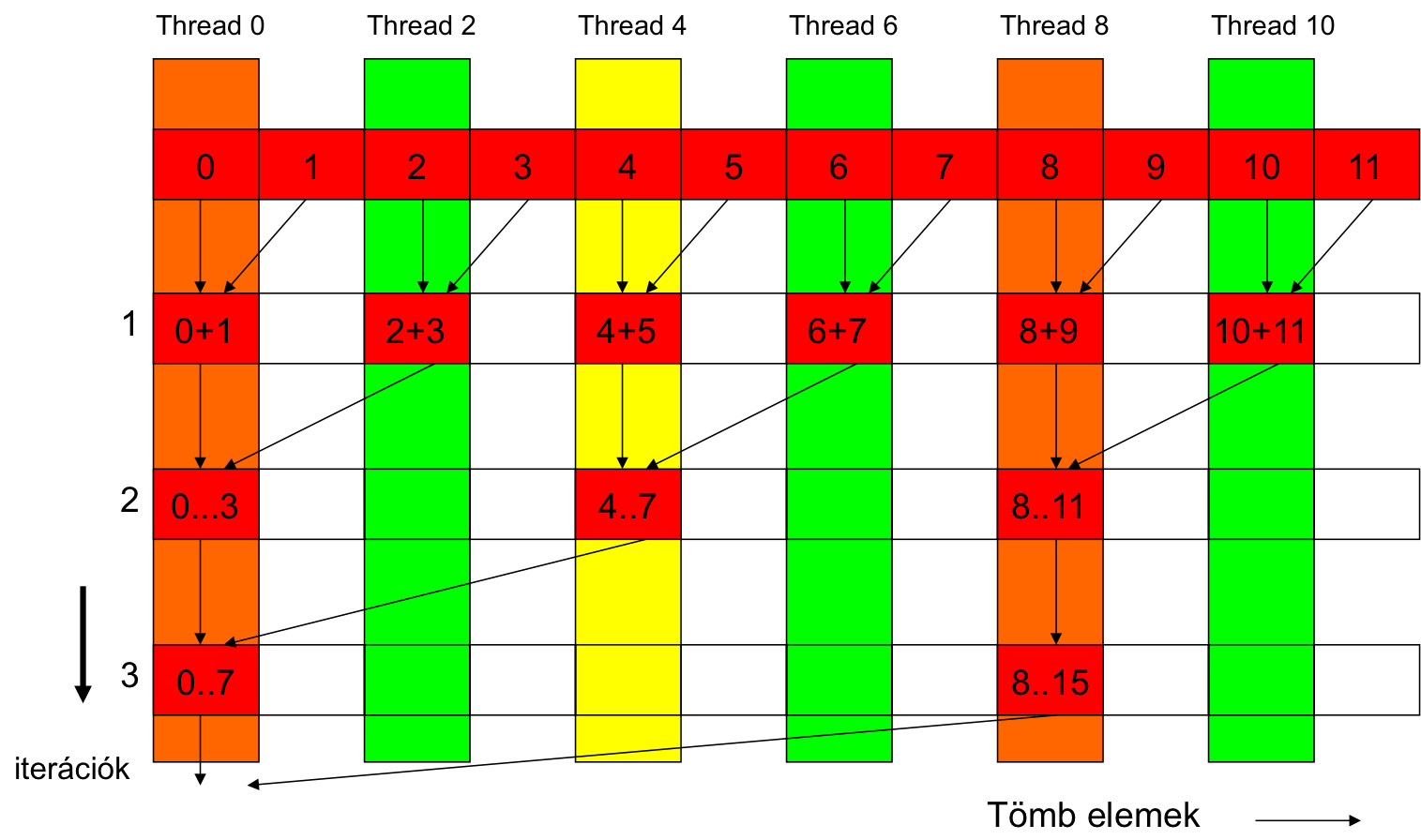
Parallel reduction

• Alaphelyzet, annyi szálat indítunk, ahány elemű a tömb.
• PROBLÉMA1: Ez pazarlás, a szálak fele csak az adatbetöltésben vesz részt -> nem dolgozik.
• PROBLÉMA2: A kernel kódban if szerepel -> szál-divergencia!
• (A nem futó szálak is elvisznek néhány órajelet).

Parallel reduction - javítás

• Nem a szomszédos elemeket adjuk össze, hanem (az egy block-on lévő) rész-tömb másik felében lévővel.
• A >> operátor a bináris jobbra shiftelés itt. (bináris számrendszer = hatékony osztás kettővel.)
• (nb.: GPU-n próbáljuk kerülni a sima osztást.)

parallel reduction - javított működés

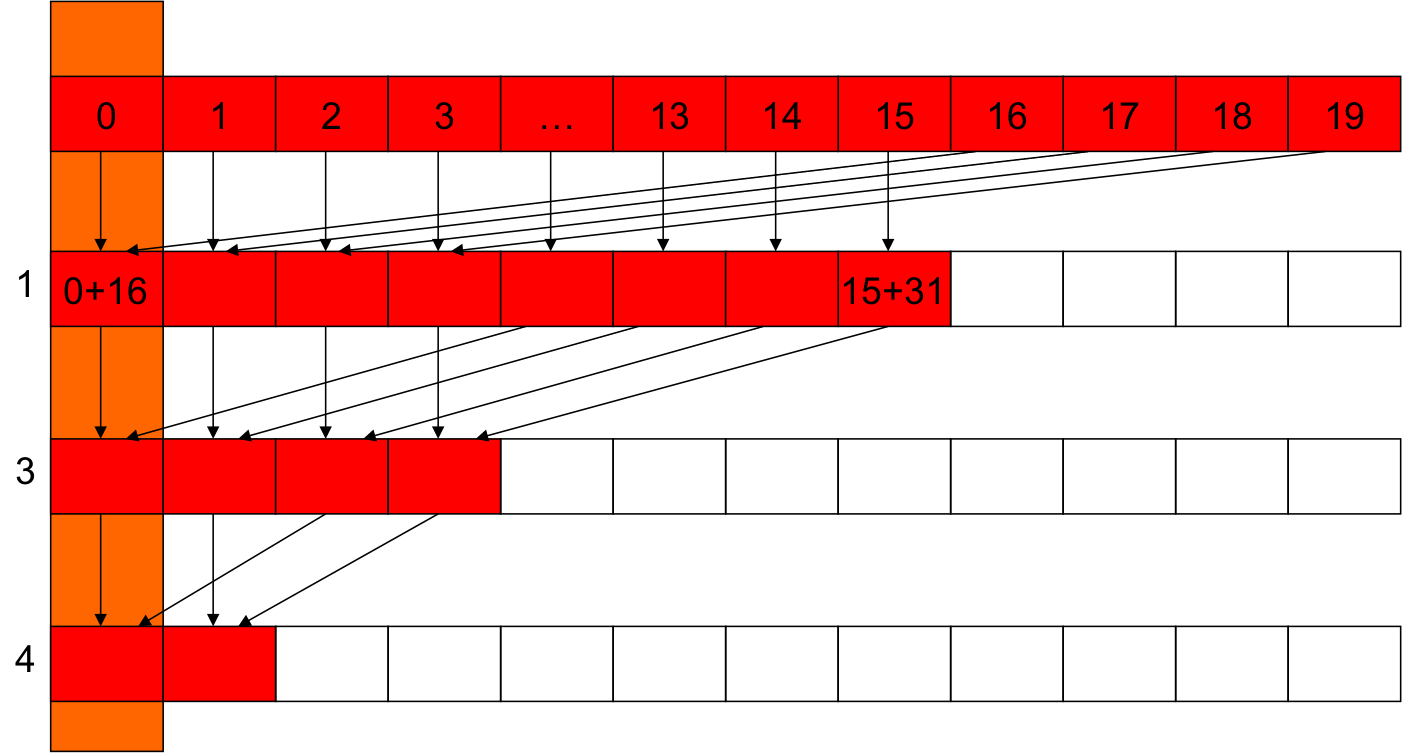
Az új működés

• Miért is jó? Még mindig van divergencia, és ugyan annyi dolgozó szál van.
• Az iterációkban egymás mellé kerülnek a futó és nem futó szálak.
• Ezáltal azonos warp-ba kerülnek -> nincs divergencia.
• (Ez az utolsó 5 iterációban nem lesz igaz - miért?)

Feladat I.

• Egészítsd ki a kódrészletet működő programmá:
• Beolvasás a shared memóriába.
• Több blokkon való futás.
• Végeredméynül visszaadja a tömb szummáját a 0-ik pozícióban.

Feladat II.

• Készítsd el a program módosított változatát:
• A kernel kód csak 1 iteráció.
• Több kernelhívással, változó futtatási konfigurációval érd el, hogy ne legyen "inaktív" szál sosem.
• Mennyivel hatékonyabb ez a program?

Tudásfelmérő:

                        
#define VECTOR_N 1024
#define ELEMENT_N 256
const int DATA_N = VECTOR_N * ELEMENT_N;
const int DATA_SZ = DATA_N * sizeof(float);
const int RESULT_SZ = VECTOR_N * sizeof(float);
...
float *d_A, *d_B, *d_C;
...
cudaMalloc((void**)&d_A, DATA_SZ);
cudaMalloc((void**)&d_B, DATA_SZ);
cudaMalloc((void**)&d_C, RESULT_SZ);
...
scalarProd<<<VECTOR_N, ELEMENT_N>>>(d_C, d_A, d_B);

__global void scalarProd(float *d_C, float *d_A, float *d_B)
{
	__shared__ float accumResult[ELEMETN_N];

	float *A = d_A + ELEMENT_N * blockIdx.x;
	float *B = d_B + ELEMENT_N * blockIdx.x;
	int tx = threadIdx.x;

	accumResult[tx] = A[tx] * B[tx];

	for(int stride= ELEMENT_N / 2; stride > 0; stride >>=1)
	{
		__syncthreads();
		if(tx < stride)
			accumResult[tx] += accumResult[stride + tx];
	}
	d_C[blockIdx.x] = accumResult[0];
}
                        
                        

Kérdések

• Hány thread lesz összessen?
• Hány thread lesz egy warp-ban?
• Hány thread lesz egy block-ban?
• Hány global memory művelet lesz thread-enként?
• Hány hozzáférés lesz a shared memory-hoz block-onként?
• Lesznek bank-conflict-ot okozó sorok? Ha igen melyek?
• A for ciklus hány iterációja lesz divergens?
• Lehet szignifikánsan csökkenteni a global memory hozzáférést? Hogyan? Hány hozzéférést lehet megspórolni?