Szonokémia kutatócsoport
Szonokémia kutatócsoport
A vegyipar az egyik legnagyobb energiafogyasztó szektor a nehéziparban. Az összes energiafelhasználás mintegy 19%-át tette ki 2012-ben az OECD államokban, ezzel ez a szektor mondható a legnagyobb energia felhasználónak. Ezért, a vegyipar mindig is fontos szerepet fog játszani a gazdasági fejlődésben és növekedésben. Nem beszélve arról, hogy a legtöbb iparágnak a vegyipar az egyik legnagyobb beszállítója. Annak ellenére, hogy az Európai Unió (EU) vegyipara kitűnő állapotban van, egyes előrejelzések a szektor növekedésének eltolódását prognosztizálják a feltörekvő országok irányába (Kína, India, Brazília, …). Ennek oka az EU-ban egyre nagyobb mértékben problémát jelentő munkaerőhiány, a sokkal szigorúbb környezetvédelmi előírások és az alapanyagok drágulása (ami a feltörekvő országokban nagy bőségben van). Ezért, bármilyen áttörés a területen segíthet enyhíteni a verseny okozta nyomást.
Fontos pár szót említeni a magyarországi specifikumokról is. Jelenleg az ország gazdasága az autóiparra épül a maga 30%-os részesedésével (2017). Ez a „monokultúra” a magyar gazdaságot rendkívül sérülékennyé teszi, mivel a gazdaság teljesítményét szinte egy ágazat határozza meg. Ha az autóipar teljesítménye jelentősen csökken, akkor az amúgy is pár százalékos GDP növekedésre jelentős hatást fog gyakorolni. Magyarországon a vegyipar részesedése kb. 8.6%, tehát egy erős alappal rendelkezik ahhoz, hogy bármilyen áttörés a szektor jelentős bővülését eredményezze. Ez a gazdaság diverzifikációját erősítené.
Az egyik lehetséges módszer, ami a szektorban áttöréssel kecsegtet az a nagy intenzitású ultrahang (harmonikusan változó, nagy intenzitású nyomástér) alkalmazása folyadékokban. Ezzel az egyes kémiai folyamatok kihozatalát jelentősen növelni lehet. Ez az új megközelítés a szakirodalomban szonokémiaként ismert. A módszer fizikai alapja a kavitáció egyik speciális esete, az akusztikus kavitáció. Lényege, hogy az ultrahangos besugárzás során mikron méretű buborékok keletkeznek, amik klaszterekbe rendeződnek. A buborékfelhők nagy skálás komplex dinamikája a lenti felvételen látható (©www.hielscher.com 2016).
A buborékfelhőben a buborékok radiális pulzálásba kezdenek, amelynek sebessége olyan gyors, amit a fenti kamerafelvétellel nem lehet rendesen megfigyelni. Nagysebességű kamerafelvétellel, 1-2 milliméteres területre fókuszálva a buborék klaszter és az egyedi buborékok dinamikája is már megfigyelhető. Ezt a lenti animáció szemlélteti, amit a göttingeni Georg-August Egyetem, Harmadik Fizikai Intézet laboratóriumában vettek fel (az intézménnyel a kutatási együttműködés már évek óta tart). A jobb oldali ábrán 776 ezer kép került felvételre másodpercenként az egyedi, jó közelítéssel gömbszimmetrikus, mikron méretű buborék viselkedésének bemutatásához! A buborékok oszcillációja során a kontrakció olyan nagy lehet (összeroppanás), hogy a buborékok belsejében a hőmérséklet elérheti a több ezer Kelvin fokot is, ezzel kémiai reakciókat indukálva. Innen ered a tudományág elnevezése is: szonokémia.
A fent bemutatott fizika az alapja számos szonokémiai alkalmazásnak. 1) A szonokémia a szerves kémiában áttörő jelentőségű lehet. Például, a szerves kémiában a kívánt vegyületek általában több reakciófázis keresztül kaphatóak csak meg (pl. gyógyszeripar), ahol mindegyik fázisban más-más kémiai anyagok vannak egymással kölcsönhatásban. Kutatók azt találták, hogy szonokémiai technológiával a reakcióláncok lerövidülnek, elég kevesebb reakciófázis a kívánt anyagok előállításához ezzel a folyamat hatékonysága jelentősen növelhető. 2) Szonokémiai reaktorokkal nagyon reaktív szabadgyököket lehet produkálni, amikkel hatékonyan lehet veszélyes anyagokat (pl. nehézfémeket) vagy baktériumokat degradálni/hatástalanítani. Vannak olyan erősen toxikus anyagok, amiket más technológiával szinte lehetetlen lenne hatástalanítani. Így a szonokémia a környezeti kármentesítésben is jelentős szerepet játszhat a jövőben. 3) A szonokémiának egy harmadik ága olyan fém nano-részecskéket (pl. TiO2) vagy nano-ötvözeteket gyártása, amik rendkívül jó katalizátorok a nagy felület térfogat arányuk miatt, és általában elengedhetetlenek a fotovoltaikus elemek gyártásához is. A fenti felsorolás nem teljes körű. A szonokémia alkalmazási köre rendkívül széles.
A fent említett, nagy értékű kémiai anyagok gyártása, ami specializált tudást és technológiát igényel, lehet a kulcs a versenyképességünk megőrzésében. A szonokémia jelenleg azonban számos kihívás előtt áll. A mi kutatócsoportunk egyik célja a szonokémia egyik legnagyobb kihívásának megoldása: az alkalmazás felskálázása ipari méretekre. A nehézséget a probléma rendkívül bonyolult fizikája és a nagyon nagyszámú faktor/paraméter okozza. Habár a méréseknek minden kutatásban nagy hangsúlyt kell kapniuk, a nagyszámú paraméter a csak labor kísérletekkel történő megközelítést alkalmatlanná teszi. A mi módszerünk a nagy teljesítményű számítástechnika (High-Performance Computing, HPC) és a gépi tanulás módszereinek (Machine Learning) bevezetése a szonokémia területére (lásd, "Használt módszerek részletei ").
Kulcsszavak: Szonokémia, buborék dinamika, GPU programozás, multi-stabilitás, nemlineáris dinamika
Egy szonokémiai reaktor részletes modellezése rendkívül összetett és bonyolult feladat. Képzeljük el, hogy egy reaktor mérete a deciméter nagyságrendben van, míg a benne keletkező több ezer buborék mérete a mikrométer tartományba esik. Továbbá, egy buborék pulzálásának periódusideje a mikroszekundumok rendjébe esik, de az erős összeroppanás és a kémiai reakciók nanoszekundumok alatt végbemennek. Egy rektor üzemeltetése során sok más fizikai jelenség zajlik le melyeknek idő- és térbeli felbontása több nagyságrendet ölel fel. Továbbá, a kezelendő paraméterek száma meglehetősen magas. Megjegyzésképpen, több besugárzási frekvenciát használva, ami egy bevett szokás, a paraméterek minimális száma a gerjesztési amplitúdók és frekvenciák, és a komponensek közti fáziseltolásokból tevődik össze. Két frekvenciás gerjesztés esetén ez egy 5D paraméterteret jelent. Nem beszélve olyan más, fontos paraméterekről, mint a buborékméret eloszlás, környezeti hőmérséklet és nyomás, továbbá a folyadék és a benne oldott gáz összetétele.
Úgy véljük, hogy a több frekvenciával besugárzott szonokémiai reaktorok jól megalapozott elméleti háttere nélkül nincs remény arra, hogy a szonokémia legnagyobb problémáját, az ipari méretűre való felskálázást, megoldjuk. Sőt, a fizikai folyamatok komplexitása és a paraméterek nagy száma miatt a nagy teljesítményű számítástechnika alkalmazása (HPC) elengedhetetlen. Ebből a szempontból a kutatás egyik fő célja, hogy kihasználva a professzionális videokártyák (GPUk) nyújtotta nagy és olcsó számítási kapacitást a HPC technikák alkalmazását meghonosítsuk a kutatási területen.
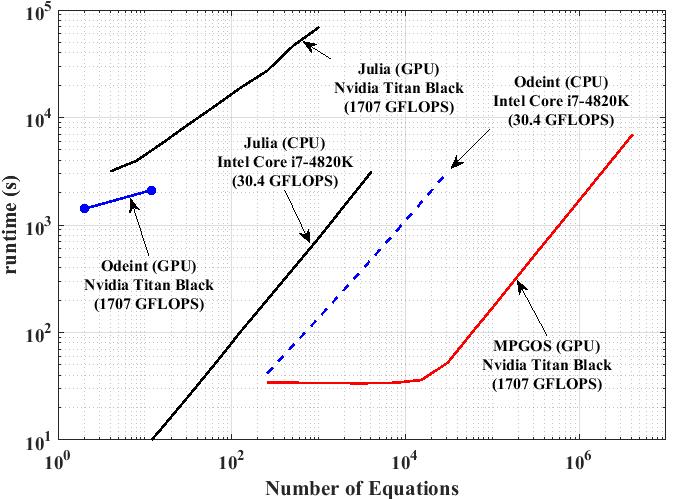
A videokártyák alkalmazásának legnagyobb nehézsége, hogy a hardware architektúrájuk kellően részletes ismerete szükséges az olyan hatékony kódok írásához, ami ki tudja használnia a bennük lévő számítási potenciált. Kutatócsoportunk egy jelentős lépést tett előre azzal, hogy egy általános célú program csomagot hozott létre, ami nagyszámú és egymástól független közönséges differenciálegyenlet-rendszereket tud megoldani párhuzamosan. A csomag nyílt forráskódú, szabadon felhasználható (MIT licensz alatt), C++ és CUDA C szoftveres környezetben íródott és a Massively Parallel GPU-ODE Solver (MPGOS) fantázianévre hallgat. A kód jelenleg a leggyorsabb GPU-ra optimalizált csomag a "piacon" szonokémiai (és több más) alkalmazásokban, amit az alábbi teljesítmény összehasonlító diagram is jól érzékeltet (a tengelyek skálája logaritmikus). A kód letölthető az alább található linkkel elérhető weboldalról. A csomaghoz tartozik egy részletes ismertető/kézikönyv számos mintapéldával.
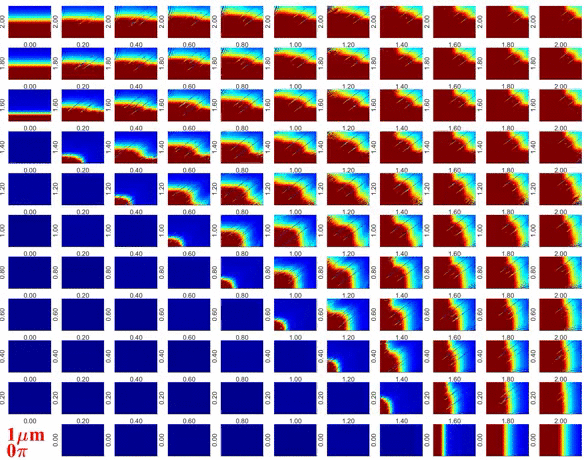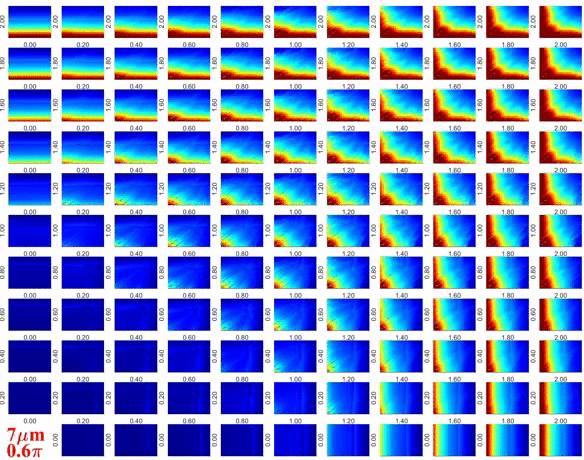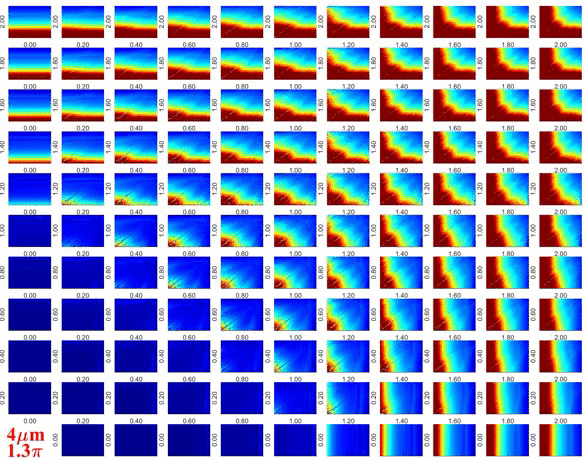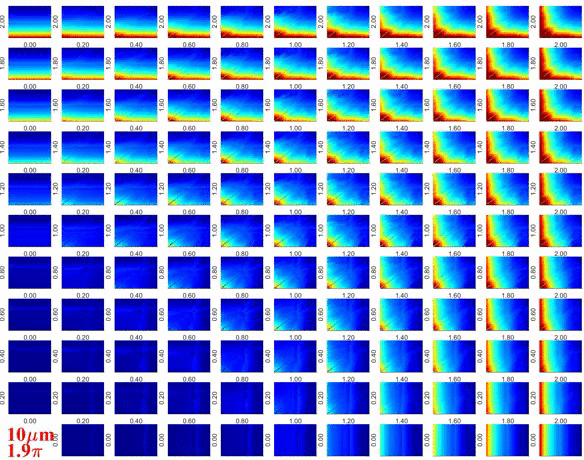
Két frekvenciával gerjesztett, egyedi buborékok összeroppanásának erőssége (becsült kémiai kihozatala) nagy felbontású, 6 dimenziós paramétertérben. Az összesen vizsgált paraméterkombinációk száma megközelítőleg 2 milliárd. A paraméterek nagy száma miatt egyszerűsített modellt használunk, ahol a kémiai kihozatalt a buborék sugár időbeli dinamikájából becsüljük. A modell a szakirodalomban jól ismert Keller-Miksis egyenlet, ami egy másodrendű közönséges differenciálegyenlet. A munka nemzetközi együttműködésen alapul az alábbi kutatóintézetekkel: Cavitation Bubble Dynamics Group, Drittes Physikalisches Institut, Georg-August-Universität Göttingen, Göttingen, Germany; Research Group Biomedical Physics, Max Planck Institute for Dynamics and Self-Organization, Göttingen, Germany; Institute for Nonlinear Dynamics, Georg-August-Universität Göttingen, Göttingen, Germany.
Az alábbi ábra egy frekvenciával gerjesztett buborék belsejében keletkező hidrogén molekulák számának keletkezését ábrázolja egy összeroppanási ciklus alatt a besugárzás amplitúdójának és frekvenciájának függvényben. Az alkalmazott modell figyelembe veszi a kémiai reakciókat a buborék belsejében, így a hidrogén termelés kihozatala pontosnak tekinthető (amennyiben a gömbi alak stabil marad). A modell bonyolultsága miatt az összesen vizsgált paraméterkombinációk száma itt jelentősen kevesebb, megközelítőleg 262 ezer. Ez is igazolja a nagy teljesítményű számítástechnika szükségesszerűségét. A kémiai reakciókinetika minél pontosabb modellezéséhez és a szonokémiai reaktorok kémiai kihozatalának minél pontosabb becsléséhez a munkát az ELTE Kémiai Intézet, Reakciókinetikai Laboratórium (Budapest, Magyarország) munkatársaival együttműködésben végezzük.
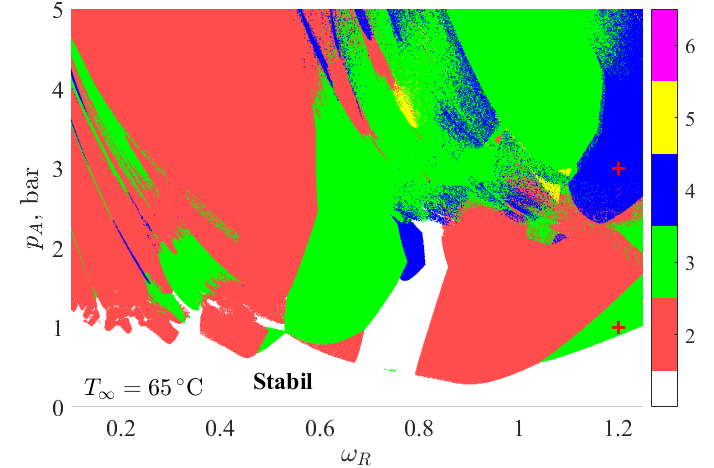
A gömbi stabilitás vizsgálata fontos az egyszerűsített modellek validáláshoz. Ha a gömbi alak instabil, akkor a buborék hosszú távon felbomlik kisebb buborékokra. Az ábrán a releváns felületi modusok (színskála) stabilitási térképe látható a gerjesztési frekvencia és a besugárzás amplitúdójának függvényében 65 fokos glicerinben. A fehér területek a stabil gömbi alak tartományai. Az alsó animációk két, gömbi alakra instabil buborék pulzálást mutatnak a 3. modusra (bal oldal, zöld szín a stabilitási térképen) és a 4. modusra (jobb oldal, kék szín a stabilitási térképen).
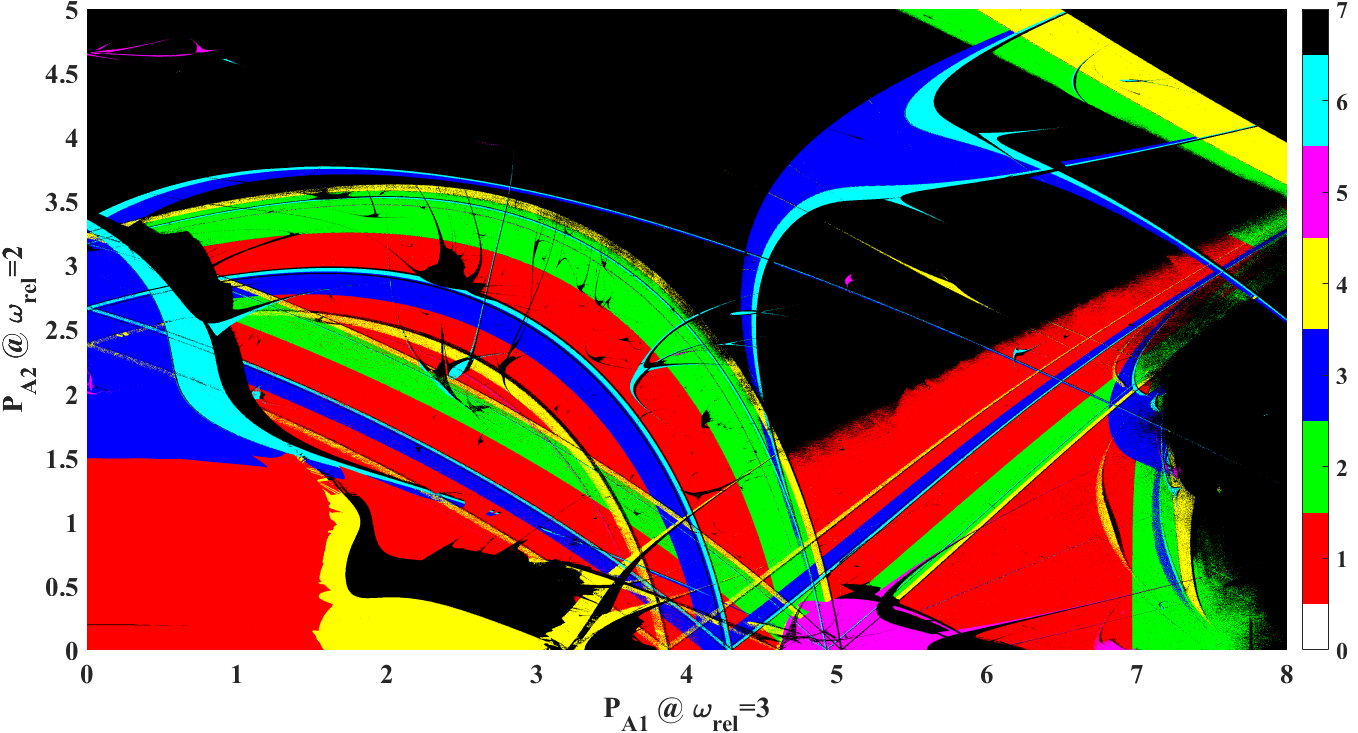
Két frekvenciával gerjesztett akusztikus kavitációs buborékok együttlétező megoldásainak feltérképezését mutatja az alábbi ábra. A különböző színekkel jelölt, egymást átfedő paraméter tartományok különböző típusú együtt létező megoldásokat jelölnek. A fontosságát a témának az adja, hogy a különbözőképpen viselkedő buborékoknak eltérő kémiai kihozatala lehet. Így fontos, hogy a rendszert olyan állapotba vezéreljük, ahol a kémiai kihozatal a lehető legnagyobb. A nagy felbontású paramétersöprés ötletet adott egy olyan visszacsatolás nélküli technika kidolgozására, amely lehetőséget nyújt a multistabilitás szabályozására úgy, hogy a kívánt stabil megoldás közvetlenül "kiválasztható".
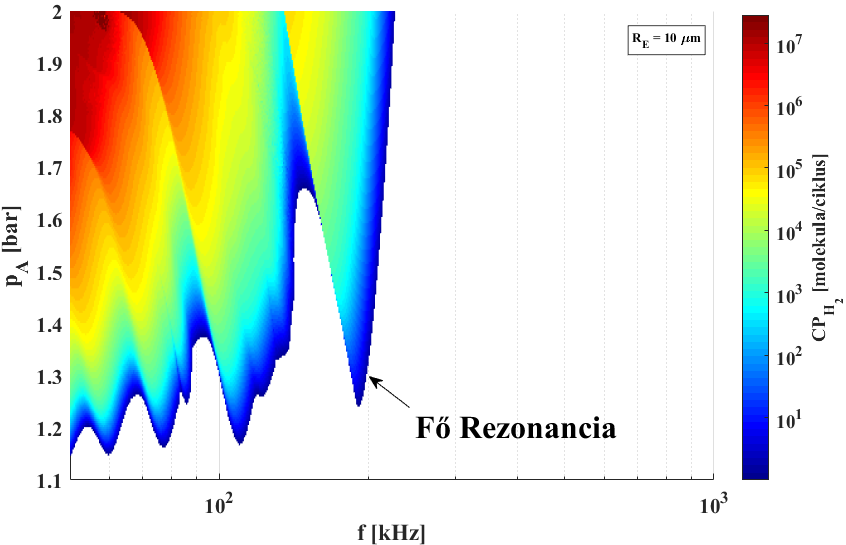
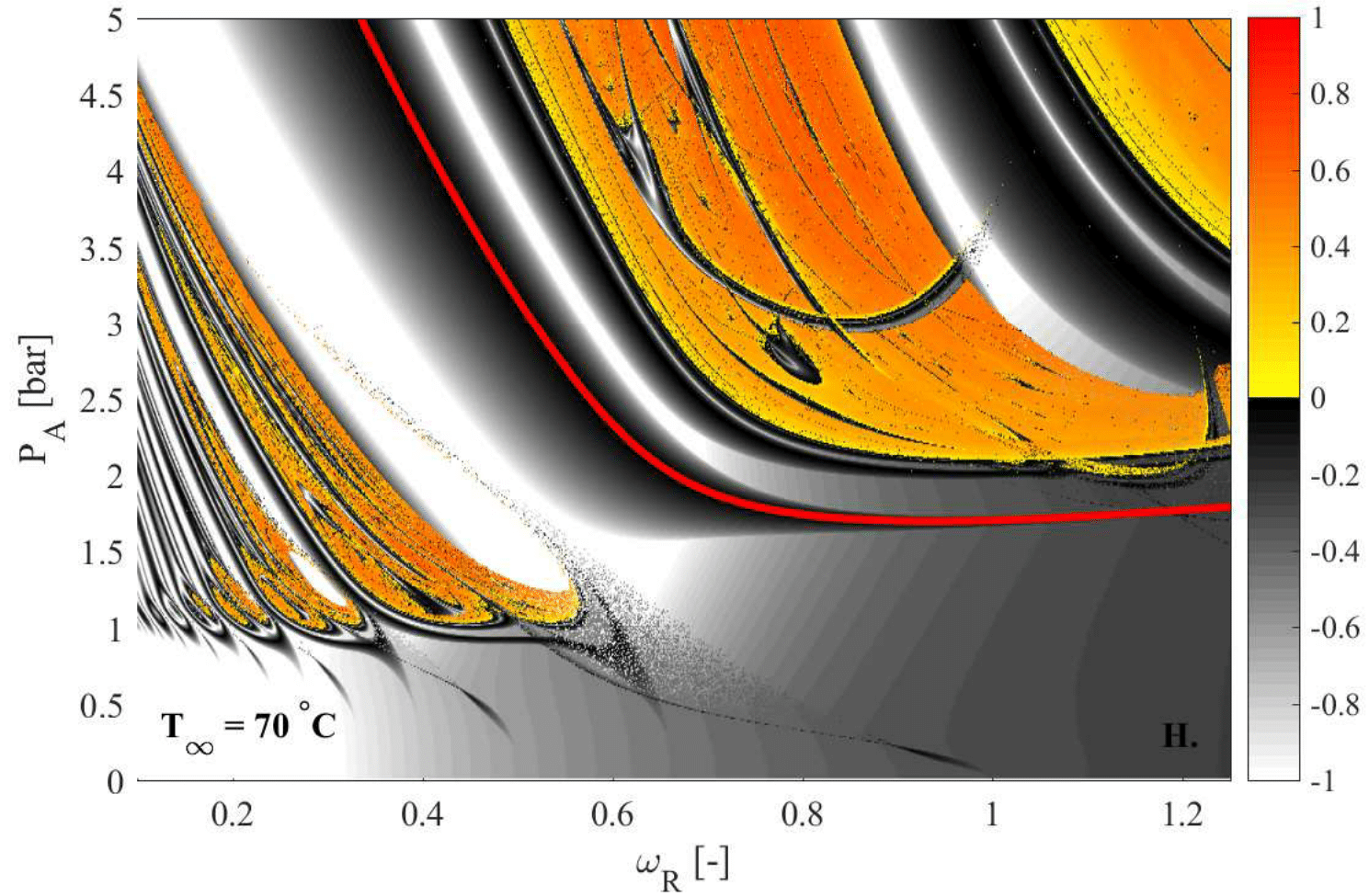
Harmonikusan gerjesztett kavitációs buborék harmonikus és szubharmonikus rezonancia tartományainak vizsgálata. A sárga területek a kaotikus, míg a szürkeárnyalatos területek a periodikus megoldásokat mutatják. Az egyes rezonáns, nagy amplitúdójú, erős összeroppanást produkáló megoldások megtalálása a szonokémia egyik fő célja. Továbbá, a kaotikus megoldások a buborékok körüli mikrokeveredést segíthetik elő, ami tovább növelheti a kémiai kihozatalt.
A gépi tanulás napjainkban rohamosan terjedő technika, ami az élet és a tudomány számos területén áttöréssel kecsegtet. Kutatócsoportunk nemrég kezdte el vizsgálni, hogy a technikát hol, hogyan és mire lehetne alkalmazni a szonokémiában. Ahogyan a GPU programozás terén egyedülálló módon értünk el sikereket a szonokémiában és általánosságban a közönséges differenciálegyenletek GPU-n való megoldásában, így a gépi tanulásos módszerek meghonosítása a kutatócsoportunkban hasonló sikerekkel járhat.
Gépi tanulást jelenleg két területen szeretnénk alkalmazni. Az első a numerikus számítások meggyorsítására irányul. Mivel már egyetlen egy buborékban lejátszódó fizikai folyamatok is rendkívül bonyolultak és számításigényesek lehetnek, így ha a numerikus számításainkat ki szeretnénk terjeszteni buborékfelhőkre, akkor az amúgy is magas számítási igény nagyságrendekkel megnőne. A célunk, hogy az egyetlen buborék viselkedését a neurális hálóval megtanulva, a buborék klaszterek számítási igényét jelentősen csökkenteni tudnánk. Fontos megemlíteni, hogy buborék klaszterek GPU-val támogatott szimulációjában már van tapasztalatunk egyszerűsített modellek alkalmazásával. Ez jelenleg is egy nemzetközi együttműködésen alapuló futó projekt (a fent említett göttingeni kutatócsoportokkal).
A másik fő terület, ahol a gépi tanulással sikereket lehet elérni az az optimális üzemeltetési stratégiák kidolgozása. Egy szonokémiai reaktor üzemeltetése során a kémiai kihozatal maximalizáláshoz az egyes paramétereket (pl. gerjesztés frekvenciája és intenzitása) nem biztos, hogy állandó értéken szabad tartani. Mivel azonban ezek a paraméterek az időben tetszőleges függvény szerint változhatnak, így a hagyományos optimalizálási eljárások nem alkalmazhatóak. Hogyan is tudnánk egy olyan üzemeltetési stratégiát kidolgozni, ahol a változtatandó paraméterek tetszőleges és ismeretlen időfüggvények? Az ötletünk az, hogy a paramétereket az időben részekre bontjuk, ahol egy időszakaszon belül a paraméterek értéke állandó, de tetszőleges lehet. Majd a gépi tanuló algoritmus megtanulja az egyes időtartományokhoz tartozó optimális paraméter beállításokat. A logika hasonló a sakkozó program tanításához: adott konfigurációhoz mi a következő legjobb lépés (következő legjobb paraméter beállítás), még ha ez akár átmenetileg a szonokémia kihozatal csökkenésével is járhat.
Ahhoz, hogy a fentiekben kitűzött kutatási célt meg tudjuk valósítani még rengeteg az elvégzendő munka. Az alábbiakban felsoroljuk (a teljesség igénye nélkül) azokat a kutatási feladatokat, amiket a következő években meg kell oldani. Ezen projektek bármelyikébe be lehet csatlakozni akár önszorgalomból, vagy szakdolgozat/diplomaterv, önálló feladat/projekt feladat és TDK kereteken belül.
Mentor program: Tudjuk, hogy senki nem úgy születik, hogy a szonokémiában, nagy teljesítményű számítástechnikában, numerikus módszerekben és a gépi tanulás eszközeiben jártas. Ezért csoportunk lehetőséget biztosít (akár már elsős féléves hallgatóknak) arra, hogy egyszerű alapfeladatokon keresztül bárki elsajátítson olyan tudást, amivel később sikeresen bekapcsolódhat meglévő kutatási irányokba. Már önmagában ez alatt az időszak alatt olyan hasznos tudásra lehet szert tenni, amit a hagyományos egyetemi képzéssel nehezen.
Új kémiai modellek tesztelése: Az, hogy milyen kémiai reakciók játszódnak le egy buborék belsejében, az az ultrahanggal besugárzott folyadék és az oldott gáz összetételétől függ. Egy-egy kémiai rendszerben rengeteg átmeneti kémiai anyag keletkezik még akkor is ha az eredeti rendszerben a komponensek száma minimális (pl. oxigén és vízgőz esetén összesen 9 komponens és 22 kémiai reakció játszik szerepet), így a modellezés általában rendkívül számításigényes feladat. Összetettebb rendszerek esetén, a komponensen száma több száz, a kémiai reakciók száma pedig több ezer is lehet. A cél, hogy különböző folyadék-gáz összetételeket modellezve és számításokat végezve feltérképezni, hogy milyen anyagok hatékony termelésére lehet alkalmas egy szonokémiai rektor. Pl. hatékony H2 termelés, CO2 lebontás, stb...
Buborékfelhők szimulációja: Egy szonokémiai rektor minél pontosabb modellezéséhez az egyik legnagyobb továbblépés a buborékfelhők modellezése jelenti. A térben lehelyezett több száz/ezer buborék egymással az általuk kibocsátott nyomáshullámokon keresztül kapcsolódnak. A paraméterek száma továbbra is nagy, minimálisan 5. Ezért első körben egy egyszerűsített buborékmodellt kell használni. A fő kérdés az, hogy hogyan lehet a nagyméretű kapcsolt rendszert olyan állapotba vezérelni, ahol a buborékok koherens (szinkronizált) összeroppanása elérhető, ami a szakirodalmi mérések szerint a kémiai kihozatalt maximalizálja.
Az akusztikus tér és a buborék klaszterek összekapcsolása: A kutatás ezen fázisa fog a legközelebb állni szonokémiai reaktorok pontos modellezéséhez. A legfőbb probléma, hogy egy szonokémiai reaktor és egy buborék mérete több nagyságrendben különbözik. Továbbá, a buborékok oszcillációja során a karakterisztikus idők is több nagyságrendben különböznek. Tehát a probléma meglehetősen nehéz, mert térben és időben több nagyságrendeket kell átfogni és kezelni. A numerikus módszernek rendkívül gyorsnak és hatékonynak kell lennie, mert a paraméterek száma továbbra is igen magas.
Egyedi buborékok minél pontosabb modellezése: Habár a jelenleg használt egyszerűsített buborékmodellek alkalmasak jó becslést adni az egyes kémiai kihozatalra, már egyetlen buborék fizikája is rendkívül bonyolult. Egyetlen buborék pontos modellezéséhez 10-100 parciális differenciálegyenletet és hozzájuk kapcsolt 100-1000 közönséges differenciálegyenletet kell megoldani (kémiai komponensek számától függ). A cél, az egyedi buborékok minél pontosabb modellezése és a pontosabb modellek fokozatos beépítése a kapcsolt akusztikus tér - buborék klaszter rendszerbe. Továbbá, a számítások felgyorsítása gépi tanulás segítségével.
Optimális üzemeltetési stratégiák kidolgozása: Az előző fejezetben ismertetett ötlet és a gépi tanulás segítségével, olyan üzemeltetési stratégiák kidolgozása, amivel a kémiai kihozatal maximalizálható. Ehhez már egy olyan modell megléte szükséges, amely képes buborékfelhők és kapcsolt akusztikus tér szimulációjára.
GPU kód fejlesztés: A fenti célok megvalósításához igen hatékony numerikus módszerek és gyors implementáció szükséges. A fő feladat, hogy a már meglévő MPGOS program kód fokozatos fejlesztésével hatékonyan támogassuk a fenti célok megvalósítását. Ez aktív C++ programozást, és a professzionális videokártyák hardver architektúrájának pontos ismeretét jelenti.
Cavitation Bubble Dynamics Group, Drittes Physikalisches Institut, Georg-August-Universität Göttingen, Göttingen, Germany.
Prof. Dr. Werner Lauterborn
Dr. Robert Mettin
Research Group Biomedical Physics, Max Planck Institute for Dynamics and Self-Organization, Göttingen, Germany.
Institute for Nonlinear Dynamics, Georg-August-Universität Göttingen, Göttingen, Germany.
Prof. Dr. Ulrich Parlitz
ELTE Kémiai Intézet, Reakciókinetikai Laboratórium, Budapest, Magyarország.
Prof. Dr. Turányi Tamás
Dr. Zsély István Gyula
Department of Mechanical Engineering, Chair of Aerodynamics and Fluid Mechanics, Technical University of Munich, Munich, Germany.
Dr. Stefan Adami
Institut für Laser und Optik, Hochschule Emden/Leer, University of Applied Sciences, Emden, Germany.
Prof. Dr. Walter Garen
Dr. Sandra Koch
2024, Kubicsek Ferenc, a Magyar Mérnöki Kamara Gépészeti Tagozatának Diplomamunka Díja
Diplomamunka címe: Mikrobuborékok kémiai aktivitása
Témavezető: Hegedűs Ferenc
2023, Kubicsek Ferenc, Felsőoktatási Mesterképzés Hallgatói Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program (ÚNKP)
5 hónapos kutatási ösztöndíj
2023, Kubicsek Ferenc, OTDK 1. helyezés
Dolgozat címe: Buborékok és ammóniagyártás
Konzulensek: Hegedűs Ferenc, Kalmár Csanád
2022, Hegedűs Ferenc, NKFI Alap - Fiatal Kutatói Kiválóság Program
Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal
4 éves kutatási ösztöndíj
2022, Hegedűs Ferenc, NVIDIA Academic Hardware Grant Program
NVIDIA Corporation
2 db RTX A5000 24GB
2022, Kozák Áron, Gábor Dénes Tudományos Diákköri Ösztöndíj
Dolgozat címe: Buborékdinamika a hidrogéngyártásban: energetikai hatékonyság numerikus optimalizációja
Konzulensek: Hegedűs Ferenc, Kalmár Csanád
2022, Kubicsek Ferenc, Felsőoktatási Mesterképzés Hallgatói Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program (ÚNKP)
10 hónapos kutatási ösztöndíj
2021, Hegedűs Ferenc, Bolyai+ Felsőoktatási Fiatal Oktatói, Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program
1 éves kutatási ösztöndíj
2020, Plavecz Lambert, Felsőoktatási Alapképzés Hallgatói Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program (ÚNKP)
5 hónapos kutatási ösztöndíj
2020, Nagy Dániel, Felsőoktatási Alapképzés Hallgatói Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program (ÚNKP)
12 hónapos kutatási ösztöndíj
2020, Kalmár Csanád, Felsőoktatási Doktori Hallgatói Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program (ÚNKP)
12 hónapos kutatási ösztöndíj
2020, Klapcsik Kálmán, Bolyai+ Felsőoktatási Fiatal Oktatói, Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program
1 éves kutatási ösztöndíj
2020, Hegedűs Ferenc, Bolyai+ Felsőoktatási Fiatal Oktatói, Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program
1 éves kutatási ösztöndíj
2020, Klapcsik Kálmán, Bolyai János Kutatási Ösztöndíj
Magyar Tudományos Akadémia
3 éves kutatási ösztöndíj
2019, Hegedűs Ferenc, Humboldt Research Fellowship for Experienced Researchers
Alexander von Humboldt Foundation
9 hónapos kutatási ösztöndíj
2019, Hegedűs Ferenc, Bolyai János Kutatási Ösztöndíj
Magyar Tudományos Akadémia
3 éves kutatási ösztöndíj
2018, Kalmár Csanád, Felsőoktatási Doktori Hallgatói, Doktorjelölti Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program (ÚNKP)
10 hónapos kutatási ösztöndíj
2018, Hegedűs Ferenc, KNORR-BREMSE, BME ösztöndíj program
Knorr-Bremse Vasúti Jármû Rendszerek Hungária Kft.
5 hónapos kutatási ösztöndíj
2018, Varga Roxána, Felsőoktatási Doktori Hallgatói, Doktorjelölti Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program (ÚNKP)
5 hónapos kutatási ösztöndíj
2018, Klapcsik Kálmán, Felsőoktatási Doktori Hallgatói, Doktorjelölti Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program (ÚNKP)
5 hónapos kutatási ösztöndíj
2017, Varga Roxána, Féléves kutatási ösztöndíj
German Academic Exchange Service (DAAD)
5 hónapos kutatási ösztöndíj
2017, Hegedűs Ferenc, KNORR-BREMSE, BME ösztöndíj program
Knorr-Bremse Vasúti Jármû Rendszerek Hungária Kft.
10 hónapos kutatási ösztöndíj
2016, Hegedűs Ferenc, Támogatás nemzetközi kapcsolatok kezdeményezésére
Deutsche Forschungsgemeinschaft (DFG)
3 hónapos vendégkutatói ösztöndíj
2016, Varga Roxána, Felsőoktatási Doktori Hallgatói, Doktorjelölti Kutatói Ösztöndíj
Új Nemzeti Kiválóság Program (ÚNKP)
10 hónapos kutatási ösztöndíj
2015, Hegedűs Ferenc, Bolyai János Kutatási Ösztöndíj
Magyar Tudományos Akadémia
3 éves kutatási ösztöndíj
Hegedűs, F., Krähling, P., Aron, M., Lauterborn, W., Mettin, R., Parlitz, U. (2020): Feedforward attractor targeting for non-linear oscillators using a dual-frequency driving technique. Chaos, 30, p. 073123.
Hegedűs, F., Klapcsik, K., Lauterborn, W., Parlitz, U., Mettin, R. (2020): GPU accelerated study of a dual-frequency driven single bubble in a 6-dimensional parameter space: The active cavitation threshold. Ultrason. Sonochem., 67, p. 105067.
Hegedűs, F., Krähling, P., Lauterborn, W., Mettin, R., Parlitz, U. (2020): High-performance GPU computations in nonlinear dynamics: an efficient tool for new discoveries. Meccanica., 55, pp. 2493-2504.
Kalmár, Cs., Klapcsik, K., Hegedűs, F. (2020): Relationship between the radial dynamics and the chemical production of a harmonically driven spherical bubble. Ultrason. Sonochem., 64, p. 104989.
Varga, R., Klapcsik, K., Hegedűs, F. (2020): Route to shrimps: Dissipation driven formation of shrimp-shaped domains. Chaos Solitons Fract., 130, p. 109424.
Klapcsik, K., Hegedűs, F. (2019): Study of non-spherical bubble oscillations under acoustic irradiation in viscous liquid. Ultrason. Sonochem., 54, pp. 256-273.
Klapcsik, K., Varga, R., Hegedűs, F. (2018): Bi-parametric topology of subharmonics of an asymmetric bubble oscillator at high dissipation rate. Nonlinear Dyn., 94(4), pp. 2373-2389.
Hegedűs, F., Lauterborn, W., Parlitz, U., Mettin, R. (2018): Non-feedback technique to directly control multistability in nonlinear oscillators by dual-frequency driving. Nonlinear Dyn., 94(1), pp. 273-293.
Hegedűs, F., Kalmár, Cs. (2018): Dynamic stabilization of an asymmetric nonlinear bubble oscillator. Nonlinear Dyn., 94(1), pp. 307-324.
Klapcsik, K., Hegedűs, F. (2017): The effect of high viscosity on the evolution of the bifurcation set of a periodically excited gas bubble. Chaos Solitons Fract., 104, pp. 198-208.
Varga, R., Hegedűs, F. (2016): Classification of the bifurcation structure of a periodically driven gas bubble. Nonlinear Dyn., 86(2), pp. 1239-1248.
Garen, W., Hegedűs, F., Kai, Y., Koch, S., Meyerer, B., Neu, W., Teubner, U. (2016): Shock wave emission during the collapse of cavitation bubbles. Shock Waves, 26(4), pp. 385-394.
Hegedűs, F. (2016): Topological analysis of the periodic structures in a harmonically driven bubble oscillator near Blake's critical threshold: Infinite sequence of two-sided Farey ordering trees. Phys. Lett. A, 380(9-10), pp. 1012-1022.
Hegedűs, F., Klapcsik, K. (2015): The effect of high viscosity on the collapse-like oscillation of a harmonically excited gas bubble. Ultrason. Sonochem., 27, pp. 153-164.
Hegedűs, F. (2014): Stable bubble oscillations beyond Blake’s critical threshold. Ultrasonics, 54(4), pp. 1113-1121.
Hegedűs, F., Koch, S., Garen, W., Pandula, Z., Paál, G., Kullmann, L., Teubner, U. (2013): The effect of high viscosity on compressible and incompressible Rayleigh—Plesset bubble models. Int. J. Heat Fluid Flow, 42, pp. 200-208.
Hegedűs, F., Hős, C., Kullmann, L. (2013): Stable period 1,2 and 3 structures of the harmonically excited Rayleigh—Plesset equation applying low ambient pressure. IMA J. Appl. Math., 78(6), pp. 1179-1195.
Koch, S., Garen, W., Hegedűs, F., Neu, W., Reuter, R., Teubner, U. (2012): Time-resolved measurements of shock-induced cavitation bubbles in liquids. Appl. Phys. B-Lasers O., 108(2), pp. 345-351.
Hegedűs, F., Hős, C., Kullmann, L. (2010): Influence of heat transfer on the dynamic response of a spherical gas/vapour bubble. Int. J. Heat Fluid Flow, 31(6), pp. 1040-1049.
Budapesti Műszaki és Gazdaságtudományi Egyetem, Gépészmérnöki Kar, Hidrodinamikai Rendszerek Tanszék
Hegedűs Ferenc, PhD (csoport vezetője)
Klapcsik Kálmán, PhD
Abu Taleb Al-Awamleh Ahmad Mahmoud Mohammed, doktorandusz
Kalmár Péter, doktorandusz
Krähling Péter, doktorandusz
Kubicsek Ferenc, doktorandusz
Nagy Dániel, doktorandusz
Kozák Áron, MSc hallgató
Oszlányi-Salacz Máté, BSc hallgató
Molnár Sára, BSc hallgató